Pseudo-Atom Molecular Dynamics

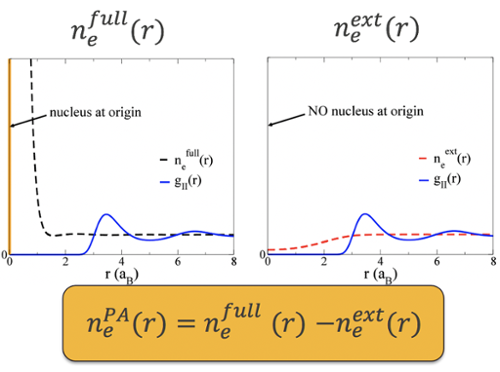
The method starts with an average atom-like calculation.  The electronic structure of a system with an external potential, created by a nucleus at the origin and a spherically averaged ion density, is found using DFT.  This gives an electron density for the 'full' system.

Next, for a system with an external potential created by the same averaged ion density, but no nucleus, another electron density is found, for the external system ('ext').

The difference between these electron densities is defined to be the the electron density due to the nucleus alone, we label this the pseudoatom ('PA') electron density.

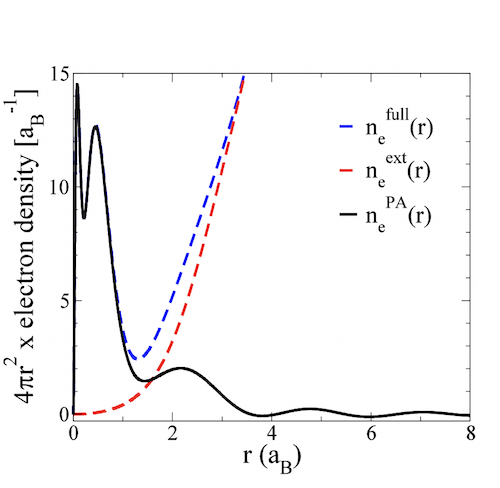
With the pseudoatom density found, the next step is to classify the electrons belonging to the pseudoatom as either bound or free electrons.  There is no unique way to do this, but physically reasonable choices give the same answers for most cases.  Where they differ is where a bound electron state lies close to the continuum of positive energy states, either in an asymptotically decaying 'bound' state, or an an asymptotically oscillating 'continuum' state.  In any case, with a reasonable choice made, we now have an ion density, and a screening density, that together make up the pseudoatom.

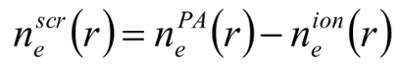
The screening density is then used as a closure for the quantum-Ornstein-Zernike equations.  With these it is possible to then define a unique ion-ion effective pair interaction potential.   This can be used in a classical molecular dynamics simulation, or if only static structure is needed, in the Ornstein-Zernike equation (to give, for example, the pair distribution function).

The average atom like calculation was first described in this paper.  A simplified model (that we now always use), is described in this work.  The PAMD model itself (i.e. the use of MD) was first published here, and equation of state applications were published here.